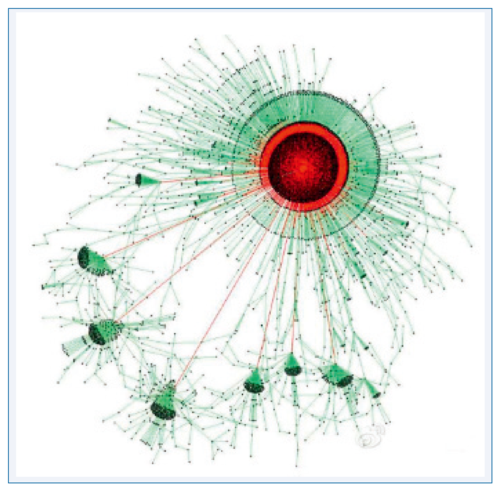
微博、微信、推特、脸书等在线社交媒体的快速发展,极大地改变了信息在网络空间中的传播过程。在线社交媒体中,每个人都是自媒体——扮演着信息生产者和信息消费者的双重角色。信息发布和传播的代价大大降低,每天有上千万甚至上亿条信息在这些平台上产生和传播。与传统的报纸、电视、网站等大众媒体的广播式传播方式不同,信息借助用户,通过好友或关注关系形成的社会网络进行传播,呈现出信息传播的级联效应—— 一个用户的信息传播行为会催发与其相连的其他用户的信息传播行为(如图1)。
图1 网络信息传播中的级联效应
在线社交媒体中的信息传播“遵循”哪些规律?我们该用怎样的模型来刻画网络信息传播的级联效应?如何从大量的信息传播轨迹中推断出用户之间的人际影响力或影响力传播网络?如何预测信息传播过程和传播范围?
对于这一系列问题的解答,不仅能帮助我们更好地理解信息在社交网络上的传播,同时也能在信息爆炸的环境下更好地服务于平台的使用者和管理者,让信息更有效地传播给对其感兴趣的用户,并对热门信息进行提前预知和管理,提升对在线社交媒体的有效利用能力和科学管理水平。
网络信息传播模型
过去几十年,大量的研究者对社交网络中信息的传播机制进行了建模和验证[1]。经典的网络信息传播模型有两种,分别为线性阈值模型[2]和独立级联模型[3]。这两个模型都假设信息的传播依赖于一个静态的网络结构,网络的节点表示用户,网络的边表示用户间的社会关系或人际影响力。不同的信息在这个静态网络中进行传播,并且每个用户在同一个信息下最多只能被激活一次。
线性阈值模型
线性阈值模型由斯坦福大学的格兰诺维特(Granovetter)提出,从信息接收者的角度来对信息传播过程建模。该模型假设网络结构中的每条边都有一个预设的人际影响力,且每个用户有一个被激活的阈值。在传播的初始阶段,有一部分用户已经被激活。在接下来的每一轮中,如果某个未激活用户周围的邻居节点中,激活用户对其的影响力大小之和超过了该用户的激活阈值,那么该用户在这一轮中就会被激活。依此类推,直到没有新的用户被激活,信息传播过程结束。
独立级联模型
与线性阈值模型不同的是,由哥伦比亚大学戈登伯格(Goldenberg)等人提出的独立级联模型是从信息传播者的角度来考虑信息传播过程的。该模型假设网络结构中的每条边都设有一个传播概率,在传播的初始阶段,有一部分用户已经被激活。在之后的每一轮中,所有上一轮被激活的用户都有一次而且仅有一次机会,以边上的传播概率激活其周围的邻居用户。当没有新的用户被激活时,该信息的传播过程就结束了。
这两个经典的信息传播模型,是对现实情况的一种简化。它只考虑信息在所有用户中一轮一轮地被同步激活,同时认为所有信息的传播所依赖的网络结构都是一样的。为了适应更复杂的实际场景,后来的研究者在这两个经典模型的基础上,进行了许多改进变形,包括从同步的激活时间到考虑连续异步的激活时间,考虑不同的内容在传播中的不同影响,将边上的影响力大小(传播概率)通过用户的表达来表示等等。这一系列针对信息传播建立的模型,可以帮助我们更好地理解信息传播的过程及其背后的机制。一方面,在这类传播模型中,通常都假设已有一个传播网络结构以及相应的传播概率,而这在真实网络中显然是不存在的。因此,有许多学者致力于通过观察大量信息的传播,来推断真实的传播网络结构和相应的传播概率。另一方面,这类传播模型也为下游的一些应用做了良好的理论铺垫,如影响最大化问题等。
传播网络推断
通常,我们只观测到信息传播的过程,而观测不到信息传播网络。例如,在微信中,我们只能看到用户在什么时间转发了某个公众号的消息,但是并不知道该用户是在哪里看到这则消息的;在疾病传播领域,我们可以获取每个患者感染疾病的时间,但很难观测到是谁传染了谁;在病毒营销1领域,我们可以获取每位顾客购买商品的时间,但很难观测到是谁向他推荐了这个商品。传播过程在我们身边时刻发生,但传播所依赖的网络拓扑结构往往难以获得。
传播网络推断问题的目标,是仅根据节点激活时间,即级联数据,推断传播网络的拓扑结构。网络拓扑结构表示为有向图。图中的点对应真实世界中的实体,如微博用户、商品客户、可被疾病感染的人群等。图中的边对应实体之间的关系,可解释为实体之间传播内容的渠道。在网络推断问题中,节点集合已知,需要推断边集。
网络推断问题的输入数据表示为级联集合。每条级联对应一条消息在网络中的传播情况。当消息、疾病等内容在网络中传播时,部分节点被激活,将在级联中记录这类节点的激活时间;部分节点始终没有接收传播内容,将在级联中标记这类节点的激活时间为+∞。
早期的网络推断研究基于传播模型同质的假设,推断结果为无权图,即假设网络中任何一对节点之间均有相同的传播概率,每条边上的权重相等,等等。例如,NetInf[4]模型即通过子模性和近似最大化方法推断无权的网络拓扑结构。带边权的网络推断模型融合了传播模型异质的假设,推断结果中的边权越大则传播概率越大、节点关系越紧密。这类方法在推断准确率上表现更好,例如通过将目标函数构造为凸问题来进行推断的NetRate[5]模型和ConNIe[6]模型。
真实世界的传播情景极为复杂,早期模型往往通过假设诸多复杂因素不存在,来降低模型的复杂度。后期的研究希望通过融合更多影响较强的因素,来提升推断的准确率。这类方法从增加考虑某些真实传播过程中的异质性的角度,来优化现有研究思路。TopicCascade[7] 模型考虑不同主题的消息在传播过程中具有不同的传播概率,使用主题模型隐含狄利克雷分布(Latent Dirichlet Allocation, LDA)获得每条消息的主题向量,进而进行网络推断。KernelCascad[8] 模型提出节点之间复杂的传播模型并不能用简单的参数模型刻画(传统方法使用的参数模型有:指数分布、幂律分布、瑞利分布),作者使用核函数表示节点间的传播模型,且不同节点对具有不同的核函数参数,进而进行网络推断。也有文章通过考虑级联异质性[9]、生命阶段异质性[10]等对网络推断方法进行优化。拥有优质、大量的级联数据是网络推断研究的基础。然而研究者所能获取的级联数据往往存在部分节点激活时间缺失的现象。针对缺失情景的网络推断方法,PSE[11] 首先对缺失级联进行处理,再进行网络推断。
网络推断领域已经取得了丰富的研究成果。但时间效率是一个亟待解决的问题。现有研究方法应对上万节点的网络时已显效率不足。除此之外,推断准确率随输入级联数据量的减小而跌势显著。如何在保证准确率的前提下缩短运行时间、降低所需级联数量,是研究者未来努力的方向。
影响最大化
社交网络中信息传播的级联效应,在一定程度上为病毒营销提供了便利和快捷。为了使广告投放利益最大化,广告商通常希望在相同的投放量下尽可能产生大的影响。换言之,我们该如何选取初始投放广告的用户,使得该广告在社交网络上获得最大的影响范围呢?基于已有的传播模型,该问题是一个NP-hard问题,暴力地遍历所有可能的解会导致时间复杂度非常高,显然不可行。如何设计一个快速有效的近似算法成为该问题求解的关键。
影响最大化问题的目标函数具有三个性质:(1)非负性——对于任意节点集合,其传播影响范围不小于0;(2)单调性——对于两个节点集合S和T,如果S是T的子集,那么T的传播影响范围一定大于等于S;(3)次模性,即边际效应递减性质——对于两个节点集合S和T,如果S是T的子集,那么任意一个不属于T的节点加入到S中,所带来的传播影响范围一定大于等于其加入到T中所带来的传播影响范围。
常用的影响最大化问题的解决方案有启发式算法[12~15]和贪心算法。启发式算法通常会根据一些启发式的规则进行种子节点的选取,速度较快,但没有精度保证。相反,贪心算法具有一定程度的精度保证,但由于其在进行种子节点选择时会通过蒙特卡洛模拟计算所有节点的边际效应,时间复杂度比较高,无法用于大规模网络。
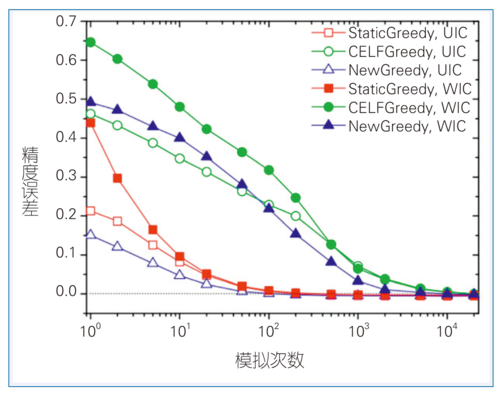
基于这一研究现状,大量研究人员致力于在有精度保证的情况下,加速贪心算法的速度。莱斯科韦克(Leskovec)等人基于原始的贪心算法,提出可以根据影响最大化问题中的次模性,避免不必要的计算,每轮只对部分节点进行蒙特卡洛模拟即可(CELFGreedy)[12]。但此时贪心算法仍然面临精度和速度之间的矛盾——由于其精度的保证取决于蒙特卡洛模拟计算影响力范围的准确性,当我们通过增加模拟次数提高算法的精度时,算法的速度会相应下降。基于这一困境,我们提出了一个静态的贪心算法(StaticGreedy)[16],即在贪心算法的迭代过程中,复用蒙特卡洛模拟的结果。传统的贪心算法中,每次迭代进行一组蒙特卡洛模拟采样,每组采样的个数必须要足够大,才能保证影响最大化问题中的单调性和次模性。而在我们的方法中,通过在迭代过程中复用这一组采样,可以用少量采样严格保证次模性和单调性,在同等精度条件下,大大降低了所需要的蒙特卡洛模拟次数。算法运行速度比经典的CELFGreedy算法快1000倍(如图2)。
图2 计算精度随模拟次数的变化情况[16]
信息传播预测
在线社交媒体中,大规模的信息在争夺人们有限的关注度,从而导致每条信息实际能够存在、活跃的时间通常都很短。因而要求我们对于信息传播的预测具有很高的时效性,算法必须能够在信息爆发或者消亡之前就能对其进行有效预测。而传统的传播模型通常都依赖于静态的网络结构,随着现实中社交网络规模的日益扩大,这类方法所需要的时间、空间代价也呈爆炸式增长,很难满足如信息传播预测这类实时性要求高的需求。因此,在信息传播的预测问题中,涌现了一批常用的轻量级方法。
在进行信息传播预测时,我们可以根据预测时间和预测目标的不同对这个问题进行不同的形式化定义。当我们在观测到信息的实际传播之前,就对信息未来的发展进行预测时,这类问题通常是真正意义上的“信息预测”;而当我们对于信息的传播进行一段时间的观测之后,再对其未来的发展进行预测时,应该更确切地称这类问题为“早期发现”[17]。这两类问题都是一般意义上的信息预测问题,而在实际的研究中,解决后一类问题的方法一般具有更好的预测表现,也就意味着更高的实际应用价值。至于信息预测的目标,通常也可以分为两类:第一类可以形式化为二分类问题——只需要给出信息在未来是否会达到某个阈值或者是否会是当前传播量的两倍等等,第二类可以形式化为回归问题——需要给出信息在未来某个时刻具体的传播量(或称为转发量)。显而易见,与第一类相比,第二类预测目标具有更大的挑战性和难度。因此,我们在实际的研究中,将更多地关注于“早期发现”预测问题并致力于提出对消息未来的传播量进行精确预测的方法。
基于特征提取的信息传播预测
基于特征提取的信息传播预测方法将信息早期发现的预测问题形式化为机器学习中的回归问题,通过提取各种类型的特征,用机器学习的方法进行模型的训练和预测。这些特征主要包括以下四类。
内容特征:指发布的信息本身。比如在新浪微博中发布的微博内容。也有研究者会对内容进行二次加工处理,包括使用LDA话题模型、情感分析模型等。
用户特征:指信息的原始发布者和转发者的相关特征。有研究发现,粉丝数多的用户所发布的信息,通常转发量也高,因此,粉丝数是用户的一个重要特征。其他用户特征包括用户之前发布过的信息、年龄、性别等。
结构特征:指社交网络的关注结构和信息传播过程中形成的传播图结构。
时序特征:包括消息在传播过程中的速度、速度变化等。
斯坦福大学的贾斯汀·程(Justin Cheng)总结并分析了已有研究中所使用的各类特征(见表1),发现时序特征最有效,在预测中占主导地位,而内容特征最弱[18]。
表1 信息传播预测中使用的各类特征
这类基于特征提取的信息传播预测方法,可以非常直观地显示哪些特征对于传播的预测是有效的,可以有助于我们理解哪些因素在传播过程中起了重要作用。但是,这类方法非常依赖人工设计的特征的好坏,而我们又没有一个统一的、具有明确指导意义的方法来指导特征的设计和提取。因此,有研究者提出用点过程来建模信息传播的过程,并在点过程中显式地建模社交网络中信息传播的几大显著特点,包括富者愈富、级联效应等。
基于点过程建模的信息传播预测
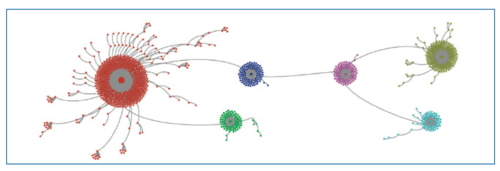
基于点过程建模的信息传播预测方法,将信息的传播积累看成是一个转发行为的到达过程,主要侧重于对每条信息转发过程中的速率函数独立建模。在研究过程中我们发现,社交网络中信息的传播主要与三个因素有关:信息本身的吸引程度,信息的吸引程度随时间衰减的速度,以及富者愈富机制(即消息的传播量越大,消息的吸引程度也越高)。在这些观察的基础上,我们率先提出了用增强泊松过程(RPP模型)来对社交网络中信息转发行为的到达过程进行建模[19]。该模型很好地刻画了信息转发行为的到达,并能快速有效地预测信息在未来某时刻的转发总量。在这一研究的基础上,我们发现一条信息的转发过程主要是由几个关键节点触发的(如图3),因此,可以通过一个混合的增强泊松过程来更好地对这样的转发过程建模,进一步提升信息传播预测的精度[20]。之后,又有研究人员提出,可以引入霍克斯自激励过程(Hawkes self-exciting process),直接通过对每一个转发带来的影响(用户粉丝数)建模,而不是用当前转发总量,以更精准化地对富者愈富的机制[21]建模。这一方法可以自然地对信息在社会网络中传播的级联效应进行建模。
图3 信息传播过程中的传播树结构
基于点过程建模的信息传播预测方法,以一种统一的框架揭示了信息级联传播背后的机制,具有较强的解释意义。但这类方法通常都是对每条信息单独进行建模,没有利用到其他信息传播过程中的丰富信息;同时,这类方法并没有直接优化要预测的目标,在一定程度上限制了其预测能力。因此,研究人员引入了端到端的深度学习框架,进一步提升了预测的准确性[22, 23]。例如,美国佐治亚理工学院的杜南(Nan Du)用神经网络的框架来自动学习信息传播过程中的速率函数[22]。最近,我们提出了DeepHawkes模型[24],在保留点过程中的几大关键解释因素的同时也引入了端到端的深度学习框架,进一步提升了预测的精度。
小结和展望
社交网络的兴起,为我们研究信息的传播提供了新的应用场景和大量的数据支持。传统的基于网络结构的信息传播建模,可以有效地揭示信息在社交网络中的传播机制,帮助我们更好地理解信息传播的过程,也为后续的影响力最大化建模提供了良好的理论基础。但是,如何能够克服日益增长的社交网络规模为这类方法带来的时间和空间上的困难,填补传播建模和传播预测之间的空缺,是我们亟待解决的一个问题。与此同时,基于特征提取和基于点过程建模的传播预测方法,为我们预测信息在未来的发展和规模提供了一种轻量级的解决方案。如何能够在这两类轻量级的方法中有效地引入社交网络中信息传播的机制和特点,考虑信息传播之间的规律共享,是我们在未来可以进一步考虑的方向。此外,信息的传播并不是一个独立的过程。不同的信息之间可能会产生相互的激励促进或竞争抑制,如何在社交网络的大环境下,同时考虑多个信息的未来发展,也是未来该领域的一大挑战。 ■
本文由国家自然科学基金项目(No.61472400、 No.61572041)资助。
注释:
1病毒营销(Viral Marketing,又称病毒式营销、病毒性营销、基因营销或核爆式营销),是利用公众的积极性和人际网络,让营销信息像病毒一样传播和扩散,营销信息被快速复制传向数以万计、数以百万计的受众,它能够像病毒一样深入人脑,快速复制,迅速传播,短时间内将信息传向更多的受众。病毒营销是一种常见的网络营销方法,常用于网站推广、品牌推广等。
参考文献:
[1] Guille A, Hacid H, Favre C, et al. Information diffusion in online social networks: A survey[J]. ACM SIGMOD Record, 2013, 42(2): 17~28.
[2] Granovetter M. Threshold models of collective behavior[J]. American Journal of Sociology, 1978, 83(6): 1420~1443.
[3] Goldenberg J, Libai B, Muller E. Talk of the network: A complex systems look at the underlying process of word-of-mouth[J]. Marketing Letters, 2001, 12(3): 211~223.
[4] Rodriguez M G, Leskovec J, Krause A. Inferring networks of diffusion and influence[J]. ACM Transactions on Knowledge Discovery from Data, 2012, 5(4): 21.
[5] Rodriguez M G, Balduzzi D, Schlkopf B. Uncovering the temporal dynamics of diffusion networks[C]//ICML, 2011:561~568.
[6] Myers S A, Leskovec J. On the convexity of latent social network inference[C]//NIPS, 2010:1741~1749.
[7] Du N, Song L, Woo H, et al. Uncover topic-sensitive information diffusion networks[C]//AISTATS, 2013:229~237.
[8] Du N, Song L, Smola A, et al. Learning networks of heterogeneous influence[C]//NIPS, 2012:2780~2788.
[9] Wang S, Hu X, Yu P S, et al. MMRate: inferring multi-aspect diffusion networks with multi-pattern cascades[C]// KDD, 2014:1246~1255.
[10] Zhao T, Song G J, He X R. Inferring diffusion networks with life stage heterogeneity[J]. SCIENCE CHINA - Information Sciences, 2017.
[11] Dou P, Du S Z, Song G J. Inferring diffusion network on incomplete cascade data[C]//WAIM, 2016: 325~337.
[12] Kempe D, Kleinberg J, Tardos É. Maximizing the spread of influence through a social network[C]//KDD, 2003: 137~146.
[13] Leskovec J, Krause A, Guestrin C, et al. Cost-effective outbreak detection in networks[C]//KDD, 2007: 420~429.
[14] Chen W, Wang Y, Yang S. Efficient influence maximization in social networks[C]//KDD, 2009: 199~208.
[15] Cheng S Q, Shen H W, Huang J M, et al. IMRank: Influence maximization via finding self-consistent ranking[C]//SIGIR, 2014: 475~484.
[16] Cheng S Q, Shen H W, Huang J M, et al. StaticGreedy: Solving the scalability-accuracy dilemma in influence maximization[C]//CIKM, 2013: 509~518.
[17] Hofman J M, Sharma A, Watts D J. Prediction and explanation in social systems[J]. Science, 2017, 355(6324): 486~488.
[18] Cheng J, Adamic L, Dow P A, et al. Can cascades be predicted?[C]// In WWW, 2014: 925~936.
[19] Shen H W, Wang D, Song C, et al. Modeling and Predicting Popularity Dynamics via Reinforced Poisson Processes[C]// In AAAI, 2014: 291~297.
[20] Gao J, Shen H, Liu S, et al. Modeling and predicting retweeting dynamics via a mixture process[C]// In WWW, 2016: 33~34.
[21] Zhao Q, Erdogdu M A, He H Y, et al. SEISMIC: A self-exciting point process model for predicting tweet popularity[C]// In KDD, 2015: 1513~1522.
[22] Du N, Dai H, Trivedi R, et al. Recurrent marked temporal point processes: Embedding event history to vector[C]//In KDD, 2016: 1555~1564.
[23] Li C, Ma J, Guo X, et al. DeepCas: An End-to-end Predictor of Information Cascades[C]// In WWW, 2017:577~586.
[24] Cao Q, Shen H W, Cen K T, et al. DeepHawkes: Bridging the Gap between Prediction and Understanding of Information Cascades[C]// In CIKM, 2017.










所有评论仅代表网友意见