2016年开启了人工智能的一个新时代。AlphaGo围棋战胜了人类，轰动性地冲击了人类的自信；微软ASR语音识别结果胜过专业速记员；斯坦福大学ImageNet的机器已能读出图像里的场景；IBM的机器沃森在日本只花10分钟就完成了对41名病人的诊断，救治了医者都束手无策的白血病人，2017年2月沃森还在天津给20位癌症病人义诊；特斯拉的自动驾驶汽车已经挤进车流；机器创作歌曲、绘画、诗歌、小说和电影等也有了不俗的成绩。现在的人工智能，已经不是几十年前哲学家争论的、影视作品中让大家熟悉的那种按规则推理的木讷机器。它更像是我们培养的智慧生物，与我们有着同源的智力。而它的核心是机器学习。我们不用告诉它怎么做，而是“喂”给它样本，让它从中汲取知识，以此自作判断。

本文意在给理工科的学者和学生介绍机器学习。只要略懂线性代数和最小二乘法的读者，便可以通过文中的数学模型和具体事例了解其机制，对涌现在我们身边第二波的人工智能有所认识。

2016年开启了人工智能的一个新时代。AlphaGo围棋战胜了人类，轰动性地冲击了人类的自信；微软ASR语音识别结果胜过专业速记员；斯坦福大学ImageNet的机器已能读出图像里的场景；IBM的机器沃森在日本只花10分钟就完成了对41名病人的诊断，救治了医者都束手无策的白血病人，2017年2月沃森还在天津给20位癌症病人义诊；特斯拉的自动驾驶汽车已经挤进车流；机器创作歌曲、绘画、诗歌、小说和电影等也有了不俗的成绩。现在的人工智能，已经不是几十年前哲学家争论的、影视作品中让大家熟悉的那种按规则推理的木讷机器。它更像是我们培养的智慧生物，与我们有着同源的智力。而它的核心是机器学习。我们不用告诉它怎么做，而是“喂”给它样本，让它从中汲取知识，以此自作判断。

本文意在给理工科的学者和学生介绍机器学习。只要略懂线性代数和最小二乘法的读者，便可以通过文中的数学模型和具体事例了解其机制，对涌现在我们身边第二波的人工智能有所认识。

机器学习

什么是机器学习？简单地说，计算机利用输入的样本，调整一个通用数学模型的参数，使得这个模型能正确地回应新的输入。这个原理在几十年前就用在模式识别上。现在计算机能力强大了，能使用巨量的模型参数和训练样本，让机器展现出令人惊异的智能，被称为机器学习。

测试人的智商(IQ)，是让被测试者回答几十道题，每道题列出几张图形，或几组数字，或几个词作为样本，让他/她从一组可能的选项中挑出一个最“合理”的答案，以此来评估此人的智商。这与被测试者拥有的知识无关，测定的是以样本作类比判断的能力。计算机的学习算法，就是模仿这种类比能力，赋予机器智商。人类具有智商，可以通过学习获得知识。计算机用调整数学模型参数的算法，实现学习的能力。样本的数据中潜藏着大量的信息，通过训练给予了机器相关的知识，让机器拥有判断这类数据的智能。

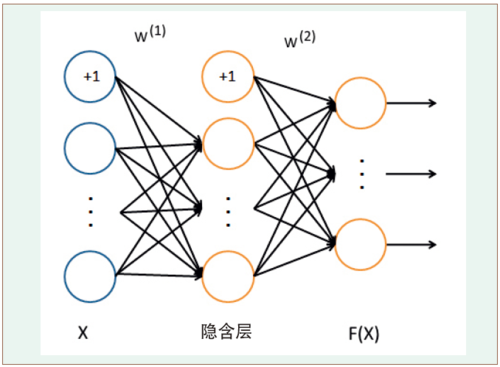
图1 神经网络

先看一个机器学习的例子。用计算机模拟400个输入节点x，10个输出节点，具有25个隐含层节点的神经网络，见图1。

这可以表示成一个从400维到10维实数值向量的函数F: R⁴⁰⁰→R¹⁰，如下：

其中神经元联接的权重和阈值w共有10285个，它们是函数的可调参数。式中的S是一个Sigmoid作用函数S(z)=1/(1+exp(-z))，让函数值分别在0或1两端饱和。

机器用它学习识别手写体字时，输入5000个各种形态图片的像素矩阵作为样本数据，每个样本是一张400个像素的手写数字图片，每个像素对应着一个输入节点，每个输出节点代表输入图片被辨识的一个类别，输出值表示图片属于这个节点类别的相似度。图片中手写所指的数字称为样本的标记，预期对应着具有最大函数值F_i的那个输出节点i的类别。不难想象，可以用最小二乘法来计算可调参数w，使得机器分类与这些样本标记的误差最小。然后可以用这个训练好的神经网络，来辨识手写数字的图片。

机器学习过程

机器的学习过程是用反向传播误差算法(backpropagation)，来迭代调整这10285个参数，这个算法由最小二乘法导出，使得输入样本的标记与对应的输出节点类别判断的平均误差最小。通过50次迭代的实验，准确率达到了95.26%。用这个调整好参数的神经网络来识别新输入的手写体数字，也取得了超过90%的预测准确率。值得注意的是，这个数学模型，即它所描述的神经网络功能，是通用的。同一个神经网络的机器，可以用它来学习识别手写体字，也可以用来区分债券的等级。对债券需要的是描述债券属性的训练样本，来供给机器学习债券的知识。同一个算法的机器，可以用不同的样本数据，赋予机器不同的知识和智能。机器的学习能力，即智商，只受数学模型对数据不同模式的表达能力所限。参数越多，表达能力越强。

通常用多元线性函数和非线性作用函数的简单组合来表示数值规律和划分类别模式，实用中的线性函数参数是以万计到百亿计的数量。这样的数学模型虽然很简单，却因参数数量的巨大，能够实现复杂的功能，从而足以涵盖各种预测和辨识情况。在数学上，这类通过调整模型参数来减少误差和应用模型预测的算法，都是精确有效的。但也因变量个数的巨大，难以分析由输入到输出每一步的变化规则，无从归纳成像物理规律那样简单明晰的因果性机制，无法用人脑跟踪逻辑推演的角度来直观地理解它的功能。

也许有人认为，既然计算机里的软件是人写的，机器不过是实现人给予的功能，怎么算是机器学习？

这种想法混淆了人赋予的功能和机器自己获得的功能。20世纪50年代的感知器(perceptron)是纯粹用硬件实现的机器学习，当时用不上计算机，更谈不上软件。那时用了400个光学传感器，以及电动机、滑动电阻和控制电路等来实现感知器，它学会辨识猫、狗和鱼等的简单图像。这个感知器相当于神经网络中的一个神经元。现代神经网络具有千万个神经元，可以实现非常复杂的辨识问题，计算机和软件只是方便地用来模拟神经网络的硬件功能的手段。现在的训练样本也同样是人供给的，但机器能通过传感器和网络自己收集样本数据，在原则上并没有什么不可克服的障碍。例如，自动驾驶汽车的机器学习，就是机器通过记录车速、油门、刹车、方向盘转角和路况的视频等，作为训练机器的样本数据。尽管如此，机器的学习功能确实是人给予的，但给予的只是学习的能力，机器通过训练的样本自己获得相关的专门知识和由此而来的智能。这就像人类，小孩是父母生养的，但知识和能力却是自己通过学习获得的。

机器学习算法

下面介绍几种典型的机器学习基础算法和事例，让读者能够想象它的功能。

无监督学习和监督学习

无监督学习和监督学习是机器学习最基本的两种类型，其他的类似于它们的综合。最常用的无监督学习是从样本数据分布中，按它们的聚集来分类。例如，用一堆新旧不同的人民币硬币的尺寸和重量作为样本的数据，分布聚集在2维空间的几个不同地方。人们看到了就知道它们是分成几类，依此知识，可以判断送来的硬币类别。机器也可以这样做，它通过数据点之间相互距离的计算(K-means)，将相近的数据点的聚集按距离自动划分成若干组。得到各组的中心和分布范围后，以此判别新输入硬币所对应的组别。许多事物看来杂乱无章，其实分属不同类别。例如，学生潜力、绘画风格和生物分类等应用对象，只要用足够多的特征属性来描述，就可以把它们区分开。但对于许多特征属性，人类只能抽取能理解其含义的少量特征，很难利用非常多的特征属性来分类，而机器却很容易做到。在人们现在的工作中，也可能应用现成的N维自动分类程序，在已经拥有的数据中发现潜藏的分类。

无监督学习就像无师自通，靠自己领悟，因此效率较差，有些情况则难以做到。有老师教学就会容易得多。监督学习是最广泛成功应用的机器学习，即用我们的知识来标记样本的正确答案，去“教”机器学会应用。

线性回归

对于数值答案的问题，线性回归是最基础的算法。几百年前，人们就用它从实验数据中导出经验公式。采用最小二乘法，可以求出与这些数据误差最小的直线或超平面。例如：

线性回归公式

这里j是输入属性的下标，i是输出向量数值分量的下标，(k)指第k个样本。它有公式解，在线性代数上称为“正规方程(normal equation)”的线性方程解。然而，商业应用中的机器学习模型，未知参数w_ij的数量巨大，公式求解要求非常大的计算机内存和计算量来实现，通常是用梯度法迭代求出近似解。这是被最广泛应用的数值预测的学习方法。

如果数据关系不能用一个线性式子表示怎么办？这可以通过增加一些与输入属性x是非线性关系的项，例如，令x₁=x, x₂=x², x₃=x³,…，有可能把它们表达成一个线性式子，即高维空间里，这些点可能放在一个超平面上，在样条函数逼近理论上，已经有许多数学研究成果。在应用上，它相当于选取足够多的输入属性表达。例如，对于房价的估值，房子所在地区和面积是基本的属性，当用线性回归预测误差较大时，可加入邻居平均房价、房间卫浴个数和装修等级等，用这些与已有属性不是线性关系的特征，来扩充属性空间的维数，有可能取得较好的模型精度。

逻辑回归

对于分类模式的判断，逻辑回归是基础的算法。在直观上是用一个超平面把输入属性空间分成两半，逻辑上分别对应0和1。超平面用一个线性函数表示，输出对应于线性函数值是否大于0。多个超平面将属性空间分成多类。能够这样归类的数据被称为是线性可分的。20世纪50年代人工智能热潮中的感知器，用一个Sigmoid作用函数加在线性函数之后，有如下表示：

逻辑回归公式

让输出结果基本饱和在0和1，并且易于用最小二乘法导出减少误差的梯度。它模拟了神经元的功能，一列组成的单层神经网络，能很好地处理线性可分的模式识别。对于不是线性可分的模式，可以采用上述增加输入特征属性的方法，让它在高维空间上线性可分。

支持向量机

支持向量机(SVM)在单层神经网络基础上，采用非线性变换φ将输入的数据向量x映射到特征属性空间，让φ(x)在特征属性空间是线性可分的。它使得线性分类器可以用在非线性分类问题上，不需要明确给出这个非线性变换，它的实现是通过直接构造与特征属性空间中内积相等的“核函数(kernel function)”来简化计算。支持向量机用分段线性函数代替神经元里的Sigmoid作用函数，这样调整间隔分类超平面的参数，就只跟较少的支持点有关了，既可以大大减少计算量，又把计算转化成二次函数在线性约束下求极值的问题。实际应用中，涉及到巨大稀疏矩阵的计算。1998年，微软研究院约翰·帕拉特(John C. Platt)提出的SMO算法，可以高效地处理巨量的变量和样本数据，这使得支持向量机获得广泛的应用。支持向量机包含单层感知器作为特例，它有清晰的数学理论的支持，能有效地控制训练结果，现在已有许多计算机语言实现的软件包可用。相对于多层神经网络，它所要求的机器资源较少，是非常实用的学习算法。但它要求有应用领域知识的人进行合作，来选取合适的核函数。它已成功地应用在许多分类领域，如文本、图像、蛋白质、垃圾邮件分类和手写体字识别等。

神经网络是多层感知器的网络，对每一层输入都用线性来分类，由于Sigmoid作用函数，每层的输入和输出是个非线性变换，不需要人为设计属性变换，便能通用地实现各种数据的分类。文章开头介绍的就是3层神经网络的一个例子。理论上，3层神经网络可以实现任何分类问题。但随着复杂程度的增加，要求中间隐藏层的神经元数会急剧地增加。每层神经网络实现一个线性分类函数，多层神经网络则实现了多重的复合函数，能大大提高学习功能，用较少的神经元解决复杂的问题。但对于多于3层的神经网络，采用反向传播误差的梯度法来统一训练，较难控制学习的结果，所以兴起深度学习的研究。

深度学习

相对于前面介绍的单纯机制的机器学习数学模型，深度学习像是一种综合的工程设计，它的基本架构是深层的神经网络，具有处理非常复杂的模式的能力。为了提高训练的效果和效率，需要设计具有不同层次的网络构造。例如，在计算机视觉领域广泛应用的卷积神经网络(CNN)，便是在低层先采用几个卷积核层和联营层来抽取特征和压缩信息，它们是“先天”预设功能的神经网络层，具有较少可调的联接参数，能自动获取局部特征，且易于控制训练的效果。在深层网络中有的还采取分层采用无监督的预先学习和随后的监督学习的方法，来提高学习效率。如何构造深度网络和控制训练是深度学习的研究内容。今天深度学习的神经网络已有百亿个神经联接参数，具有极高的智商，它需要巨大的计算机资源和信息数据的支持，多在大公司用于研究突破性的应用和探索人工智能的未来。

20世纪80年代，计算机的功能还不多，不及现在的手机。当时手写体字识别的研究应用上述例子中的神经网络来学习，限于计算机的功能和收集数据的能力，只用几百个样本逐个迭代更新参数来学习，这样无论计算多少个小时，结果都不理想。现在用5000个样本，同一个神经网络模型用批量计算更新参数，经过50轮迭代，在个人电脑运行不到10分钟，模型就训练好了。注意，这里用的只是简单的拥有400×25×10个节点的三层网络，已经有了1万多个待定的参数，输入样本是400×5000的矩阵。这个辨识10个数字图像的小项目，在过去很难实现，现在做起来却很轻松。现在，机器学习进入了与人类智能相当的时代。斯坦福大学ImageNet的机器学习，用了1500万张照片的数据库，涵盖22000种物品，对2400万个节点、150亿个联接的神经网络进行训练，能够让计算机看懂照片，描述图里的场景。这个成果证明了在巨量的样本数据和强大的计算能力支持下，凭借着上述非常简单的数学模型的学习机制，便能够使机器通过训练，从白痴达到具备令人惊异的辨识认知能力。现在，深度学习的成就还只是验证概念的破冰式探索，如何构造深度神经网络，如何更有效地利用数据和已有知识更聪明地进行学习，例如具有长期、短期记忆的神经网络，“利用上下文或背景知识判断”等等，正在竞相研究中。

机器学习强大的功能来自巨量的可调参数，它的学习算法并不难理解，基本上是向量和矩阵的线性运算，关键之处是获取巨量的样本数据，和支持巨量计算的硬件，特别是GPU等技术进步。这就是为什么机器学习的突破，一直到了大数据时代才出现。